Kenneth Edwards, Michael A. Allen*
open access article published in The Fibonacci Quarterly 58(5), 128–134 (2020)
Abstract
We consider the tiling of an n-board (an n×1 rectangular board) with third-squares (1/3×1 tiles with the shorter sides always aligned horizontally) and (1/3,2/3)-fence tiles. A (w,g)-fence tile is composed of two w×1 subtiles separated by a g×1 gap. We show that the number of ways to tile an n-board using these types of tiles equals Fn+13 where Fn is the nth Fibonacci number. We use these tilings to devise straightforward combinatorial proofs of identities relating the Fibonacci numbers cubed to one another, to other combinations of Fibonacci numbers, and to the Pell numbers. Some of these identities appear to be new. We also show that for p=2,3,…, the number of ways to tile an n-board using either 1/p×1 tiles and (1/p,1−1/p)-fences or (1/2p,1/2−1/2p)- and (1/2p,1−1/2p)-fences is Fn+1p.
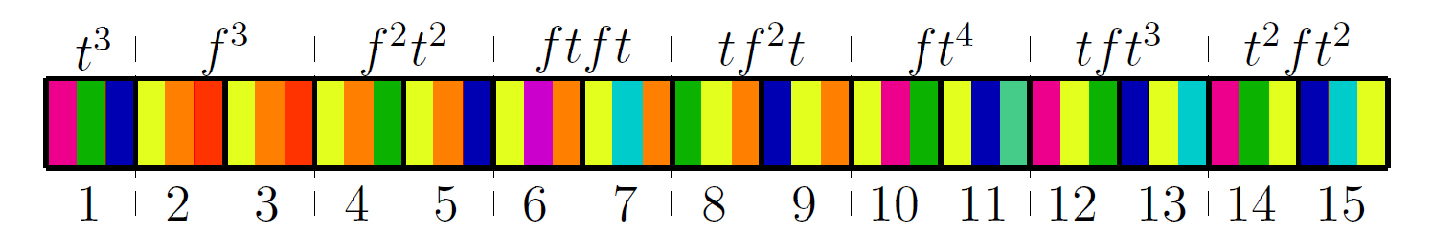
Background
Enumerating tilings of finite boards can give a physical picture of various integer sequences. For example, the number of ways to tile an n-board (a linear array of n square cells) with squares and dominoes is the Fibonacci number Fn+1 where Fn=Fn−1+Fn−2+δn,1, Fn<1=0. These combinatorial interpretations can be used to give quick intuitive proofs of identities instead of using algebra. A tiling which includes fractional length tiles and/or tiles with gaps, such as fence tiles, can be reduced to a tiling using metatiles. A metatile is a grouping of tiles that exactly covers an integer number of cells and cannot be split into smaller metatiles. Evaluating the number of metatiles of a given length is the key to obtaining convolution-type identities via this class of combinatorial interpretation.
Key results
• Two new combinatorial interpretations of Fnp for p=2,3,….
• A new method for enumerating metatiles of a given length.
• 7 new identities relating Fn to the Pell numbers Pn (where Pn=2Pn−1+Pn−2+δn,1, Pn<1=0). E.g.,
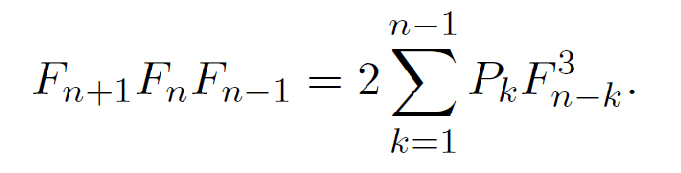
Related publications
[1] Sloane NJA (2010) The Online Encyclopedia of Integer Sequences, oeis.org.
[2] Benjamin AT, Quinn JJ (2003) Proofs That Really Count: The Art of Combinatorial Proof, Mathematical Association of America.
[3] Edwards K (2008/2009) A Pascal-like triangle related to the tribonacci numbers. Fibonacci Quart 46/47(1), 18–25.
[4] Edwards K, Allen MA (2019) A new combinatorial interpretation of the Fibonacci numbers squared. Fibonacci Quart 57(5), 48–53.
[5] Edwards K, Allen MA (2020) A new combinatorial interpretation of the Fibonacci numbers squared. Part II. Fibonacci Quart 58(2), 169–177.