In a magnetic system system, frustration implies the situation in which all spin-spin interactions can not be satisfied simultaneously, in a sense that all bonds cannot be in the lowest-energy state. One example is the frustration due to the underlying geometry of the spin network, the so-called geometric frustration. The intrigue consequence that makes this type of systems interesting is that a classical ground state will be suppressed, which as a result gives an opportunity for a quantum state to emerge at low temperatures.
One can suppress the classical ground state and enhance quantum fluctuations by reducing the connectivity of spin-spin interactions by reducing dimensionality of the spin network. For example, the connectivity of the spin network in one dimensional is two but increase to 4 in a two-dimension square lattice. The lower the dimensionality the better chance the system will host a quantum state. Therefore, in our group we are also interested in low-dimensional magnets and looking for interesting spin dynamics in this group of materials.
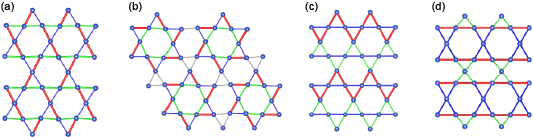
For the frustrated magnetic system, our group is currently working on a kagome lattice antiferromaget. The kagome lattice is a triangle-based spin network, comprised of corner sharing triangles. Coupled with the antiferromagnetic interaction, the bonds around each triangle cannot be simultaneously satisfied, giving rise to frustration. A family of compounds that we are studying is A2Cu3BF12, where A is a monovalent ion Cs or Rb, and B is a tetravalent ion Sn, Ce, Hf, Zr, or Ti. At room temperature, the majority of the compounds in this family are reported to crystalize in the rhombohedral crystal system, where Cu2+ ions form a perfect kagome plane comprising equilateral triangles. However at low temperatures, the systems undergo a structural phase transition, causing the kagome plane to become distorted. The figure below show examples of distorted kagome planes results from the phase transition.
For the low dimensional magnets, our group is working on a number of systems, which form a network of spin chains.
Related work
"Magnetic structure of the distorted kagome lattice antiferromagnet Cs2Cu3SnF12, " K. Matan, T. Ono, G. Gitgeatpong, K. de Roos, P. Miao, S. Torii, T. Kamiyama, A. Miyata, A. Matsuo, K. Kindo, S. Takeyama, Y. Nambu, P. Piyawongwatthana, T. J. Sato, and H. Tanaka, Physical Review B 99, 224404 (2019). [link] [arXiv:1905.01454]
“Large Negative Quantum Renormalization of Excitation Energies in the Spin-1/2 Kagome Lattice Antiferromagnet Cs2Cu3SnF12,” T. Ono, K. Matan, Y. Nambu, T. J. Sato, K . Katayama, S. Hirata, H. Tanaka, J. Phys. Soc. Jpn. 83, 043701 (2014). [link] [arXiv:1311.1875]
“Ghost modes and continuum scattering in the dimerized distorted kagome lattice antiferromagnet Rb2Cu3SnF12,” K. Matan, Y. Nambu, Y. Zhao, T. J. Sato, Y. Fukumoto, T. Ono, H. Tanaka, C. Broholm, A. Podlesnyak, G. Ehlers, Physical Review B 89, 024414 (2014). [link] [arXiv:1305.4042]
“Pinwheel VBS state and triplet excitations in the two-dimensional deformed kagome lattice,” K. Matan, T. Ono, Y. Fukumoto, T. J. Sato, J. Yamaura, M. Yano, K. Morita, and M. Tanaka, Nature Physics 6, 865 –869 (2010). [link] [arXiv:1007.3625]